Can AI solve game theory problems?
Chat GPT attempts to solve a repeated game
I am teaching game theory this fall and looking for ways to integrate AI/LLMs. In a previous post, I shared how ChatGPT solved a Coordination Game. Today we examine how well Chat GPT4 does when solving an indefinitely repeated game.
An indefinitely repeated game is one that, well, repeats indefinitely. The games get interesting if it is a situation where cooperation is not the right move when the game is played once, but can become the right strategy when the game is repeated.
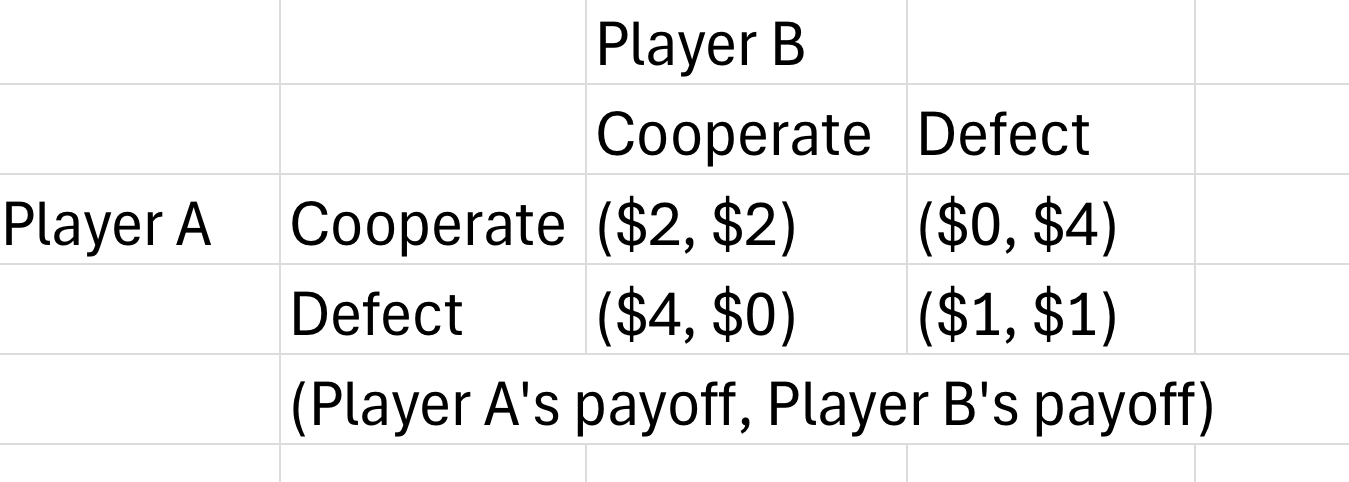
Consider this following game:
In this game, if played once each player has an incentive to defect, earning more ($4 or $1) by defecting than by cooperating ($2 or $0). The problem is that if both cooperate, both get $2 which is better than the equilibrium when both earn $1. This is a prisoner's dilemma game, often studied in introductory economics.
That’s what happens if the game is played only once. It is interesting is when this game is repeated, however, because there is a chance cooperation can work. It all depends on how much the future is valued or discounted.
I asked ChatGPT about this game and again, Chat GPT’s analysis was spot on!
I wrote: "Let's play a game. Suppose that you could get $2 every time period indefinitely if you cooperate with "player 2" and they also cooperate. (You are player 1). If you both defect, you both get $1. If you defect and they cooperate, you get $4. The game repeats except that there is a 10% chance the game ends after each period. Your opponent faces the exact same payoffs. Your opponent is intelligent and doesn't make mistakes in analysis. Do you choose to cooperate or defect in period 1?
The response:
This is a repeated Prisoner’s Dilemma with a geometric probability of continuation. Let’s solve it step-by-step.
Payoffs:
Both cooperate: each gets $2
Both defect: each gets $1
You defect, opponent cooperates: you get $4, they get $0
You cooperate, opponent defects: you get $0, they get $4
Continuation Probability:
The game continues with 90% probability each round, so the discount factor (δ) = 0.9
Strategy Considerations:
The opponent is intelligent and makes no mistakes. Let’s assume the opponent is using a grim trigger strategy: they will cooperate as long as you do, but defect forever if you ever defect.
This creates an incentive to maintain cooperation unless the temptation to defect is too large.
Calculate Expected Value of Cooperating:
If you cooperate every round:
VC=21−δ=21−0.9=20.1=20V_C = \frac{2}{1 - \delta} = \frac{2}{1 - 0.9} = \frac{2}{0.1} = 20VC=1−δ2=1−0.92=0.12=20Calculate Expected Value of Defecting in Period 1:
If you defect in period 1, you get $4 in the first round, but the opponent will defect forever afterward (assuming grim trigger). So in future periods, you both get $1.
VD=4+δ⋅11−δ=4+0.9⋅10.1=4+0.9⋅10=4+9=13V_D = 4 + \delta \cdot \frac{1}{1 - \delta} = 4 + 0.9 \cdot \frac{1}{0.1} = 4 + 0.9 \cdot 10 = 4 + 9 = 13VD=4+δ⋅1−δ1=4+0.9⋅0.11=4+0.9⋅10=4+9=13Comparison:
Cooperate: $20
Defect: $13
Conclusion:
You should cooperate in period 1. The present value of long-term cooperation exceeds the short-term gain from defection, given the 90% continuation probability and the assumption of a rational opponent using grim trigger (or similar punishment-based strategy).
Once again, I am impressed at how well it can solve the games, and how well it can articulate the results for why a particular action should be taken.